This lesson will cover some additional observations and insights regarding voting methods that should help clear away some confusion.
Only RCV (ordinal) methods must reduce to Plurality in two-candidate elections; Cardinal methods can do much better: Everyone will agree that voters can, and normally do, have a wide range of opinions about candidates. Opinions will range from strong approval of some candidates to strong disapproval of others. Somewhere toward the middle is indifference, that is, the voter doesn’t either like or dislike a candidate. It also is very possible that some voters are indifferent about a given candidate because they have never heard of that candidate or just don’t know enough to have an opinion one way or the other (it turns out that there normally are quite a lot of these “no opinions”— in the range of 35% of all voter-candidate opinions). No-opinions should not affect the choice of a winner.
Unfortunately, there is no way to reach into voters’ minds and obtain an accurate and sincere measure of how strongly they may approve or disapprove of each candidate. Instead we must ask them to indicate their opinions on a ballot of some sort. Collecting the data in this manner loses the calibration of the absolute scale of approval/disapproval. It also gives voters the option to lie (vote strategically) about the strengths of their opinions (and other aspects as well). This is an unfortunate and severe degradation of the data that are available to voting methods! (There may be some acceptable ways to gather more accurate data from voters on an absolute scale, but that topic is for another course.)
There is, however, one point on the approve/disapprove scale that can be preserved and which supports comparing voters’ opinions to a useful extent on an absolute basis. That is the “no-opinion” point, which we might call absolute zero.
If a voting method only allows voters to compare candidates relative to each other, we lose any tie to the absolute approve/disapprove scale. If a voter says A is better than B, we have no idea whether that voter thinks A and B are both great candidates with A being better than B, or whether A and B are both horrid candidates with B being some amount more horrid than A. Any tie to the absolute approve/disapprove scale has been lost. Absolute zero is lost. This is important information. Without it, the large number of “no-opinions” might (depending upon a voting method’s design) improperly affect results instead of just being disregarded. Without it, there is no sure way to tell if, when, or which candidates have (positive) net approval over all voters or (negative) net disapproval. This is rather crucial since no voting method should be able to ever make the horrible blunder of choosing a winner that the majority of voters disapprove!!
Considering only two-candidate elections, all ordinal methods must reduce to Plurality because (other than not voting at all) there are just two possible valid ballot configurations: either candidate A is better than B, or B is better than A. Remember that the strength (magnitude) of voters’ opinions is important. Cardinal methods can provide voters a way to convey at least some rudimentary information about the strengths of their opinions, as well as whether the opinions are favorable or unfavorable (instead of just relative to other candidates). For that reason, they are able to more accurately and more often identify the correct winners. For a good example, AADV (in addition to not voting at all) has seven possible valid ballot configurations. Using any ordinal method’s ballot, a voter can convey only one bit of information, while a voter using an AADV ballot can convey nearly three bits of information.
The “Transform Trap:” “Normal” scoring methods allow each voter to assign one of their scale’s values to each candidate, and then identify the winner as the candidate with the highest total score. Suppose that such a scoring method employs a three-valued scale of -1, 0 and +1. Those reasonably accomplished in mathematics will quickly realize that any affine transform can be applied to the scale without affecting how the scoring method functions. For example, a scale of 0, 1, 2 or 1, 2, 3 or -30, -10, +10 could just as well be used and would not change the operation of the scoring method.
Both AADV and BAWV utilize a three-valued “scale” of -1, 0 and +1. Math wizards may fall into the trap of thinking that the AADV and BAWV scale can be similarly transformed without changing the behavior of these two methods. That is incorrect.
AADV and BAWV are not “normal” scoring methods. They are decidedly different. Each voter does not assign one of the scale values to every candidate. Instead, these methods operate by counting the number of voters who have indicated that each candidate is the best candidate and also the number of voters who have indicated that each candidate is the worst candidate. The “score” for each candidate is the number of voters who have chosen that candidate as best minus the number of voters who have said that the candidate is the worst (just as it is with any “Yes/No” referendum). The candidate with the highest net positive “score” is the winner.
Note that voters are empowered to reject all of the candidates if they don’t like any of them. This is one of the most important advantages of these two methods. It is what strongly discourages the nomination of polarizing candidates. Both methods maintain the ability to consistently identify the correct winner when there are many candidates (typical for primary elections). The use of AADV or BAWV for primary elections would make it highly unlikely for candidates with high negatives to win and appear in general elections.
There is yet another important consideration. In any election, there are very many instances where a voter has no opinion about some specific candidate. This might occur because the voter just doesn’t feel strongly one way or the other, but more often, it happens because a voter simply does not know enough about a candidate to even have an opinion. In elections with more than two candidates, typically 35% of all voter-candidate opinions are “no opinion” (that’s a lot). A “no opinion” must not affect the choice of a winner in any way. All no-opinions are quite correctly ignored completely by AADV and BAWV. The typical score method has no way to distinguish between a no opinion and a negative opinion. See the discussion in the immediately preceding section about losing track of “absolute zero.”
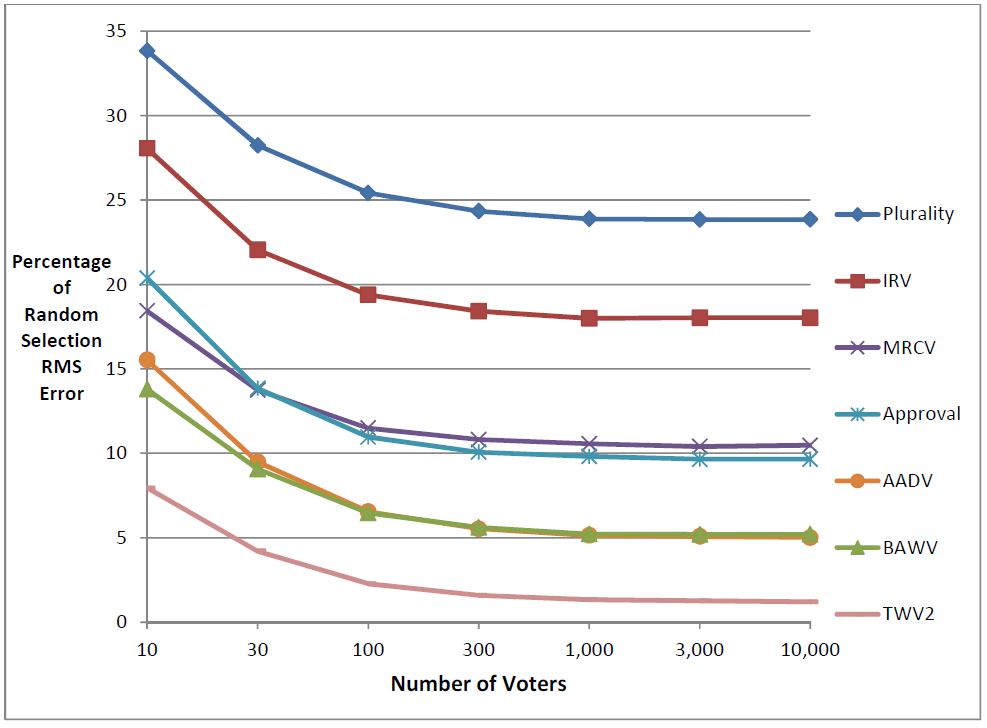
On the resolution of scoring scales: A perfect voting method would be able to gather sincere voters’ opinions for each candidate on a high resolution scale; the 201 integers from -100 to +100 would work extremely well. Such a fictitious voting method would be able to identify the correct winner in every election, regardless of the number of candidates or the number of voters. Because of strategic voting, we know that we can only utilize a low resolution scale, such as the three integers, -1, 0 and +1. The statistics of large numbers of voters can, in large measure, make up for the low scale resolution. However, it should be expected then that voting methods which use low resolution scales will make more mistakes when there are small numbers of voters. This phenomenon was investigated for four-candidate elections using election simulations. All voting methods tested stabilized at their best performance when there were more than 1,000 voters. For that reason, all other data for election simulations was gathered with more than 1,000 voters (typically 10,000). All the voting methods exhibited increasing errors with fewer than 1,000 voters. These results are shown on the chart below.
Nominating “clone candidates” (and similar attempts to manipulate elections): The specter is often raised of political parties attempting to manipulate election outcomes by, for example, nominating a “dummy” candidate (or assisting a more obscure candidate) similar to an opponent’s candidate in order to split the vote (siphon off some of the opponent’s votes). Such attempts actually are modifying the nature of the election itself – that is, altering the selection of candidates from which voters must choose the best one. The definition of the best candidate to win is the one which maximizes voter satisfaction net of dissatisfaction when summed over all those who voted. That is still true whether or not there are clone candidates present. It is true for any candidate configuration. All such candidate configurations can also occur legitimately, of course, so there could be no way for a voting method to tell when it’s an attempt to manipulate and when it’s a normal occurrence. It would be wrong and dangerous to try to engineer a voting method to deliberately pick some winner other than the one voters think is best. Whether or not parties can effectively manipulate elections, it is still up to voters to decide which candidate is best. All a voting method can do is most accurately and consistently identify the candidate that is the voters’ choice. To the extent that cloning (etc.) is a serious problem, the solution to it does not lie with the voting method. Note that the universe does not provide a guarantee that every problem must have a great solution, or even any solution at all.

Responses