When Messrs. Condorcet and Borda warned of Plurality’s pernicious deficiencies (late 1700s) and proposed alternative voting methods, a great debate began. An academic paper-writing “industry” has flourished for centuries (not to mention Nobel prizes). Why, then, is the use of Plurality still so pervasive? Many thousands of person-years of effort have not resulted in a strong consensus choice of a really good replacement for Plurality.
There are many factions arguing for one method or another. Two main “cults” seem to have emerged, one advocating Instant Runoff Voting (IRV) and one insisting that Approval Voting (AV) is superior. A smaller faction pushes Score Voting and there are lots more. However, no one is able to conclusively argue that their method is a better replacement for plurality than all others.
Axiomatic Approach The predominant approach over the centuries has been to write down a set of axioms that a voting method should satisfy. Each axiom excludes various members of the set of all voting methods and it is hoped that at least one remains standing at the end of the process. The chosen axioms then are the definition of “best possible decision,” not the straightforward definition stated in lesson 2. This could be useful, but seems like a rather indirect approach. Of course, the selection of axioms is crucial. The predominant focus has been on the ordinal, or ranked-choice methods.
An axiom which certainly should be included in any collection is simply that no candidate for whom total voter satisfaction is negative should be able win an election. A weaker version might also be acceptable: No candidate that a majority of voters dislike should ever win an election. It does not appear that such an axiom has ever been a feature of the axiomatic approach. The reason may be that no ranked-choice method can satisfy this axiom.
Miscellaneous Efforts A plethora of other methods, both ordinal and cardinal, have been proposed, some of them rather complex. Typically, multiple hypothetical election scenarios are constructed to illustrate and study how a method handles them. Analyzing how methods deal with so-called election paradoxes is popular. However, there is no definitive way to extrapolate from a necessarily finite set of hypothetical election scenarios to the substantially infinite number of possible real-world election scenarios. The “arguments” necessarily are just “hand-waving” arguments. Therefore, there has been no way to prove that one method is superior to another in the many possible actual public elections with large numbers of voters.
Data-driven Approach The problem we face is a statistical one. We need to find the voting method which most accurately and consistently identifies the correct winner in all possible types of elections, and does not make horrible blunders in any type of election. Those who are physicists or engineers tend to have an annoying penchant for insisting upon, you know, some actual data to confirm or refute a hypothesis, or to guide further inquiry. However, acquiring reliable and useful data from real elections is extremely difficult. Furthermore, gathering the large volume of data required to have confidence in conclusions for such a huge statistical problem is prohibitively daunting and hazardous.
Fortunately, modern digital computers provide a powerful tool to model entire complex elections and to quickly gather detailed statistics on any desired aspect to any reasonable statistical significance. It is entirely practical to test many voting methods and compare them quantitatively. Some forms of strategic voting can easily and accurately be simulated; other kinds can be simulated with more effort and risk. For simulated elections, we actually do have a “satometer” since each voter/candidate opinion (or utility) is generated, therefore known. It is as though we have an X-ray or a CT machine and can see inside elections and gain a much better understanding of what is important and what is not. Of course, any such simulation requires, begins with and depends upon a concise definition for the best choice.
Surprisingly, it appears there has been little serious effort in this area. It appears that the first such project was done circa 2000 by Warren D. Smith, but it unfortunately had some known problems and shortcomings. How elections are simulated obviously does matter. More recently, there was an investigation in 2019 and one in 2020 done by Roy Minet. Those produced a plethora of intriguing results which certainly pass the common sense test. Complete information regarding both of these projects can be found here: http://royminet.org/voting-elections/
Election Simulation Results The chart below shows the statistical characteristics of 600,000 simulated elections of all possible kinds with 10,000 voters voting in each of the elections. All voters voted sincerely in these simulations. The 600,000 were divided into batches of 100,000 elections each, where each batch had a different number of candidates running. Races having 2 through 7-candidate were evaluated.
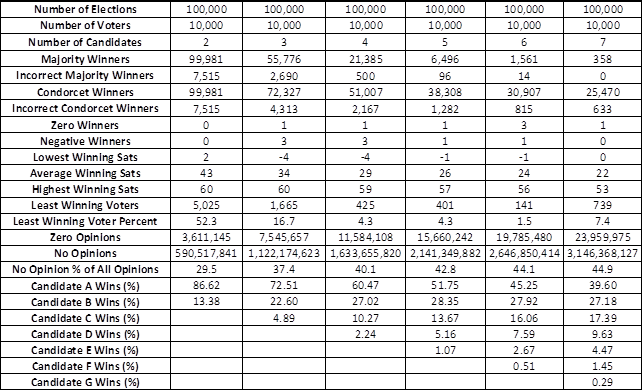
There is no guarantee that these statistics would exactly match those of 600,000 actual elections, but everything certainly looks entirely plausible and no anomalies have been found.
Looking just at the column for 4-candidate elections, take note of a few things in particular. In 21,385 of the 100,000 elections, one of the four candidates had a majority of the votes and would be the winner if the Plurality or IRV voting method were being used. However, 500 (2.3%) of those majority winners were not the correct winner (using the Lesson 2 definition). This is as expected. Similarly, there were 51,007 Condorcet winners, but 2,167 of those were not the correct winner. Since all majority winners also are Condorcet winners, we must subtract them from the total Condorcet winners to obtain the number of Condorcet winners who were not also majority winners; there were 29,622 of those and 1,667 (5.6%) were not the correct winner. In an election with 4 candidates and 10,000 voters, there will be 40,000 opinions of candidates. In 100,000 such elections there will be 4 billion opinions. More than 1.6 billion of those (over 40%) were “no opinion,” meaning that the voter does not know enough about that particular candidate to even have an opinion! This seems quite realistic and is something that voting methods need to “take in stride.”
The chart below shows how successful various voting methods are at identifying the correct winner. In order to have a measure of each voting method’s performance that is independent of the way the simulation was done, a “standard voting method” was included for comparison. The “standard voting method” simply selects one of the candidates at random. The percentages on the chart show what percentage of the random selection error each method had; that is, how much better each method is at identifying the correct winner than just randomly selecting one of the candidates. Obviously, random selection would be 100% on this chart for any number of candidates while a perfect method would be zero percent for any number pf candidates.

It should be no surprise that Plurality is the worst method. For two-candidate races it has 12% (about one eighth) the error of just randomly picking a candidate. However, its performance degrades quite rapidly when there are more than two candidates and it has 33% (about one third) of the error of random selection when there are seven candidates. Bear in mind that the chart shows performance with all voters voting sincerely. Considering its large vulnerability to strategic voting (voting for the “lesser evil”), Plurality’s error will increase even more rapidly than shown on the chart in real-world elections whenever there are more than two candidates.
Instant Runoff Voting (IRV) is always identical to Plurality for two-candidate races. It does offer some modest improvement for more than two candidates and is at 22% for seven candidates. However, IRV is less susceptible to strategic attack, so its performance would not be expected to degrade quite as rapidly in real-world elections as does Plurality’s when there are more than two candidates.
Note that Pairwise Comparison was measured with IRV as the “fallback method” to be used in elections where there is no Condorcet winner. The performance of this complex kludge was substantially identical to that of IRV. In spite of the huge amount of attention lavished upon it, Condorcet’s clever idea does not appear to have much merit. Perhaps this should not be too surprising since a Condorcet winner is a weaker criterion than a majority winner (which also is a Condorcet winner – a much stronger one), and even some majority winners are not the correct winner. Also, for many elections, there simply is no Condorcet winner.
Approval Voting (AV) offers a significant improvement over Plurality and IRV. It has only 4% of random selection error for two candidates and 16% for seven candidates. Since AV should be expected to have essentially the same susceptibility to strategic voting as IRV, AV is decisively to be preferred over IRV.
Several other ranked-choice methods (not shown) were tested. Their performance always fell between IRV and Approval Voting. The performance of the best ranked-choice method closely matched (but was not quite as good as) AV, which is the simplest cardinal method. There is no proof for this, but it certainly appears that no ordinal (ranked-choice) method can be better than or equal to AV. That is, all the better performing methods will be cardinal methods.
Down at the bottom of the chart are two new voting methods developed as a part of the 2020 simulation project: AADV and BAWV. The most significant difference is that both of these methods allow voters to express their dissatisfaction for some candidates, while the other methods limit voters to expressing only satisfaction.
It was learned from the simulations that the single datum most helpful to choosing the correct winner is indeed the voters’ choice of the candidate they think is best. However, coming in a close second is voters’ choice for the candidate they think is worst. It was also learned that, after those top two data, not many voters have additional information to offer; and when they do, the additional information only very slightly improves the accuracy of picking the correct winner.
To summarize, the better performing methods will be cardinal methods and the better performing cardinal methods must allow voters to express dissatisfaction for some candidates.
Approve/Approve/Disapprove (AADV) is even better than AV. It is at 3% for two candidate elections and, remarkably, stays under 5% for any number of candidates (2 through 7). It might be thought of as a much improved AV.
Best/Alternate/Worst Voting (BAWV) is the best voting method yet devised. It is at only 2% for two-candidate elections, 4% for three-candidates and 5% for four through 7 candidates. It can be thought of as a much improved IRV.
Both AADV and BAWV minimize their vulnerability to strategic voting by collecting the two most important data items from voters and very little more. A second approval (AADV) and an alternate best choice (BAWV) are allowed in order to eliminate or greatly reduce the motivation to vote for a “lesser evil.” Allowing any additional voter inputs could be expected to degrade performance; we know additional data cannot help decision-making very much, so it could only be harmful noise and/or attempts to manipulate results through insincere “strategic” inputs.
We do not know that AADV and BAWV are the best possible voting methods, but they are so good that we can see that there is not a whole lot of room left for further improvement. Both methods score candidates on a three-valued scale, -1, 0 and +1. Error could be further reduced by additional “resolution.” For example, a five-valued scale (-2. -1, 0, +1, +2) would help. However, we do not increase resolution because we know voters will then tend to vote strategically and predominantly use only -2, 0 and +2.
But Are Simulation Results Valid? That is, of course, a very pertinent question. We know that how elections are simulated certainly does matter. Both the 2019 and 2020 investigations simulated elections in the same way. It is encouraging that all statistics and characteristics of these elections certainly are consistent with each other and in line with what one would expect. All insights gained and results obtained seem to easily pass the common sense test. But the “bottom line” is that there (so far) is no conclusive way to be sure how well the results obtained by simulating elections apply to real-world public elections.
The technique of simulating elections seems to have enabled rapid progress toward completely unraveling a 250-year-old conundrum. It has produced two dynamite voting methods. It would obviously be good for others to independently confirm, refute or refine the results of the 2019/2020 investigations. There are many more aspects of elections that could be probed, so it is hoped that this work will be carried out in the near future.
However, at the end of the day, it really does not matter how a problem is solved. A solution is a solution no matter how it may have been obtained. Thus, the next (and last) lesson will much more closely examine the AADV and BAWV voting methods as solutions for Plurality’s woes, and that will not depend at all on the validity of election simulations.

Responses